FFTLibrary

2021年10月26日

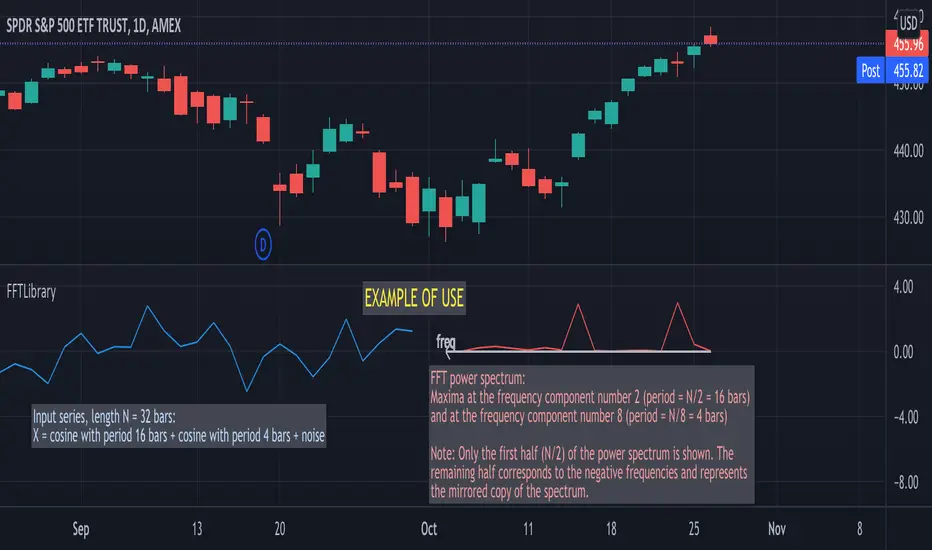
Library "FFTLibrary" contains a function for performing Fast Fourier Transform (FFT) along with a few helper functions. In general, FFT is defined for complex inputs and outputs. The real and imaginary parts of formally complex data are treated as separate arrays (denoted as x and y). For real-valued data, the array of imaginary parts should be filled with zeros.

FFT function

fft(x, y, dir) : Computes the one-dimensional discrete Fourier transform using an [url=paulbourke.net/miscellaneous/dft/
 ]in-place complex-to-complex FFT algorithm. Note: The transform also produces a mirror copy of the frequency components, which correspond to the signal's negative frequencies.
  Parameters:
    x: float array, real part of the data, array size must be a power of 2
    y: float array, imaginary part of the data, array size must be the same as x; for real-valued input, y must be an array of zeros
    dir: string, options = ["Forward", "Inverse"], defines the direction of the transform: forward" (time-to-frequency) or inverse (frequency-to-time)
  Returns: x, y: tuple (float array, float array), real and imaginary parts of the transformed data (original x and y are changed on output)

Helper functions

fftPower(x, y) : Helper function that computes the power of each frequency component (in other words, Fourier amplitudes squared).
  Parameters:
    x: float array, real part of the Fourier amplitudes
    y: float array, imaginary part of the Fourier amplitudes
  Returns: power: float array of the same length as x and y, Fourier amplitudes squared

fftFreq(N) : Helper function that returns the FFT sample frequencies defined in cycles per timeframe unit. For example, if the timeframe is 5m, the frequencies are in cycles/(5 minutes).
  Parameters:
    N: int, window length (number of points in the transformed dataset)
  Returns: freq : float array of N, contains the sample frequencies (with zero at the start).