OPEN-SOURCE SCRIPT
Boness 1964 Option Pricing Formula [Loxx]
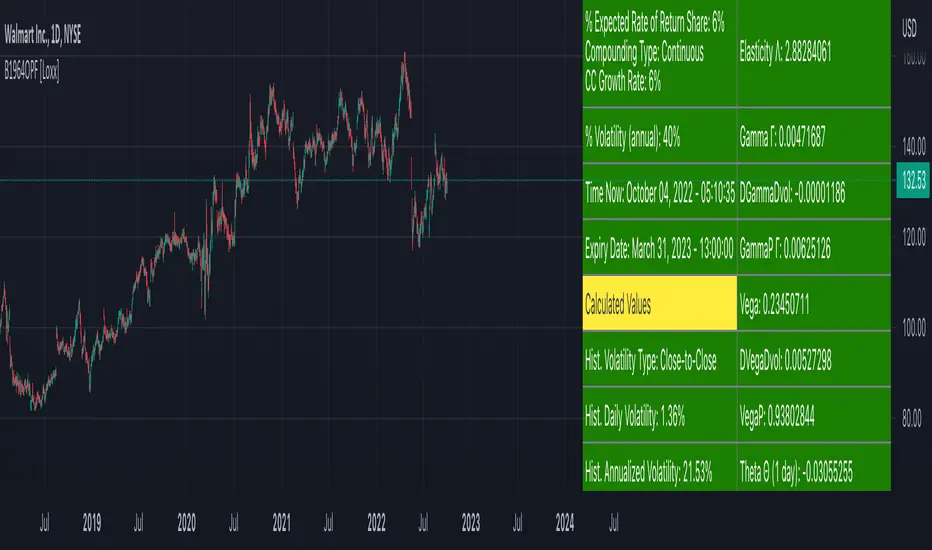
Boness 1964 Option Pricing Formula [Loxx] is an options pricing model that pre-dates Black-Scholes-Merton. This model includes Analytical Greeks.
Boness (1964) assumed a lognormal asset price. Boness derives the following value for a call option:
c = SN(d1) - Xe^(rho * T)N(d2)
d1 = (log(S / X) + (rho + v^2 / 2) * T) / (v * T^0.5)
d2 = d1 - (v * T^0.5)
where rho is the expected rate of return to the asset.
Analytical Greeks
Inputs
S = Stock price.
X = Strike price of option.
T = Time to expiration in years.
r = Expected Rate of Return
v = Volatility of the underlying asset price
cnd (x) = The cumulative normal distribution function
nd(x) = The standard normal density function
convertingToCCRate(r, cmp ) = Rate compounder
Things to know
Boness (1964) assumed a lognormal asset price. Boness derives the following value for a call option:
c = SN(d1) - Xe^(rho * T)N(d2)
d1 = (log(S / X) + (rho + v^2 / 2) * T) / (v * T^0.5)
d2 = d1 - (v * T^0.5)
where rho is the expected rate of return to the asset.
Analytical Greeks
- Delta Greeks: Delta, DDeltaDvol, Elasticity
- Gamma Greeks: Gamma, GammaP, DGammaDvol, Speed
- Vega Greeks: Vega , DVegaDvol/Vomma, VegaP
- Theta Greeks: Theta
- Probability Greeks: StrikeDelta, Risk Neutral Density, Rho Expected Rate of Return
Inputs
S = Stock price.
X = Strike price of option.
T = Time to expiration in years.
r = Expected Rate of Return
v = Volatility of the underlying asset price
cnd (x) = The cumulative normal distribution function
nd(x) = The standard normal density function
convertingToCCRate(r, cmp ) = Rate compounder
Things to know
- Only works on the daily timeframe and for the current source price.
- You can adjust the text size to fit the screen
开源脚本
秉承TradingView的精神,该脚本的作者将其开源,以便交易者可以查看和验证其功能。向作者致敬!您可以免费使用该脚本,但请记住,重新发布代码须遵守我们的网站规则。
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
免责声明
这些信息和出版物并非旨在提供,也不构成TradingView提供或认可的任何形式的财务、投资、交易或其他类型的建议或推荐。请阅读使用条款了解更多信息。
开源脚本
秉承TradingView的精神,该脚本的作者将其开源,以便交易者可以查看和验证其功能。向作者致敬!您可以免费使用该脚本,但请记住,重新发布代码须遵守我们的网站规则。
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
免责声明
这些信息和出版物并非旨在提供,也不构成TradingView提供或认可的任何形式的财务、投资、交易或其他类型的建议或推荐。请阅读使用条款了解更多信息。