OPEN-SOURCE SCRIPT
Torben Moving Median
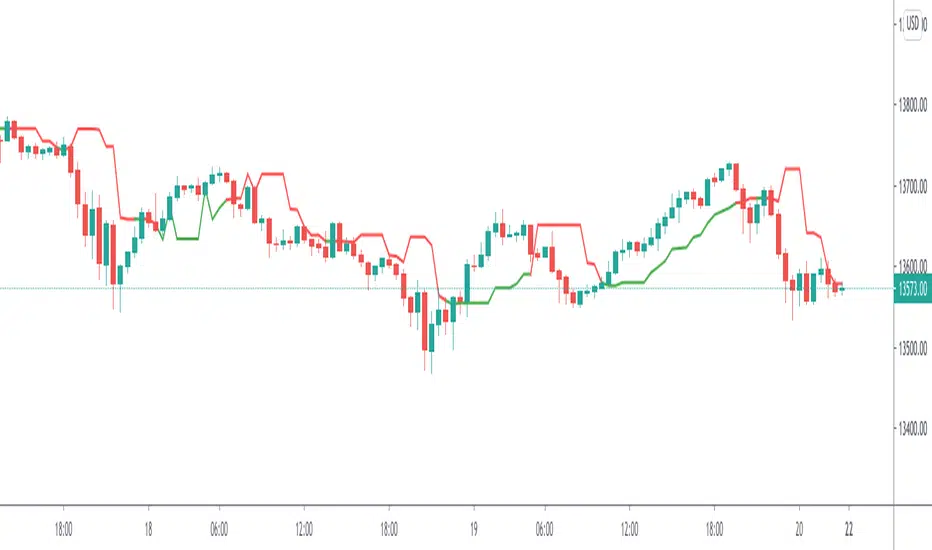
This method was pointed it out by Torben Mogensen.
It is certainly not the fastest way of finding a median, but it has the very interesting property that it does not modify the input array when looking for the median. It becomes extremely powerful when the number of elements to consider starts to be large, and copying the input array may cause enormous overheads. For read-only input sets of several hundred megabytes in size, it is the solution of choice, also because it accesses elements sequentially and not randomly. Beware that it needs to read the array several times though: a first pass is only looking for min and max values, further passes go through the array and come out with the median in little more time. The number of iterations is probably O(log(n)), although I have no demonstration of that fact.
What is Median Filtering
Median filtering is a commonly used technique in signal processing. Typically used on signals that may contain outliers skewing the usual statistical estimators, it is usually considered too expensive to be implemented in real-time or CPU-intensive applications.
Let us define the median of N numerical values by:
The median of a list of N values is found by sorting the input array in increasing order, and taking the middle value.
The median of a list of N values has the property that in the list there are as many greater as smaller values than this element.
How To trade
Trading is quite intuitive
Buy when the Price breaks-out the price which breaked the Torben Moving Median
It is certainly not the fastest way of finding a median, but it has the very interesting property that it does not modify the input array when looking for the median. It becomes extremely powerful when the number of elements to consider starts to be large, and copying the input array may cause enormous overheads. For read-only input sets of several hundred megabytes in size, it is the solution of choice, also because it accesses elements sequentially and not randomly. Beware that it needs to read the array several times though: a first pass is only looking for min and max values, further passes go through the array and come out with the median in little more time. The number of iterations is probably O(log(n)), although I have no demonstration of that fact.
What is Median Filtering
Median filtering is a commonly used technique in signal processing. Typically used on signals that may contain outliers skewing the usual statistical estimators, it is usually considered too expensive to be implemented in real-time or CPU-intensive applications.
Let us define the median of N numerical values by:
The median of a list of N values is found by sorting the input array in increasing order, and taking the middle value.
The median of a list of N values has the property that in the list there are as many greater as smaller values than this element.
How To trade
Trading is quite intuitive
Buy when the Price breaks-out the price which breaked the Torben Moving Median
开源脚本
秉承TradingView的精神,该脚本的作者将其开源,以便交易者可以查看和验证其功能。向作者致敬!您可以免费使用该脚本,但请记住,重新发布代码须遵守我们的网站规则。
Get Ocs Ai Trader, Your personal Ai Trade Assistant here
→ ocstrader.com
About me
AlgoTrading Certification, ( University of Oxford, Säid Business School )
PGP Research Analysis, ( NISM, SEBI )
Electronics Engineer
→ ocstrader.com
About me
AlgoTrading Certification, ( University of Oxford, Säid Business School )
PGP Research Analysis, ( NISM, SEBI )
Electronics Engineer
免责声明
这些信息和出版物并非旨在提供,也不构成TradingView提供或认可的任何形式的财务、投资、交易或其他类型的建议或推荐。请阅读使用条款了解更多信息。
开源脚本
秉承TradingView的精神,该脚本的作者将其开源,以便交易者可以查看和验证其功能。向作者致敬!您可以免费使用该脚本,但请记住,重新发布代码须遵守我们的网站规则。
Get Ocs Ai Trader, Your personal Ai Trade Assistant here
→ ocstrader.com
About me
AlgoTrading Certification, ( University of Oxford, Säid Business School )
PGP Research Analysis, ( NISM, SEBI )
Electronics Engineer
→ ocstrader.com
About me
AlgoTrading Certification, ( University of Oxford, Säid Business School )
PGP Research Analysis, ( NISM, SEBI )
Electronics Engineer
免责声明
这些信息和出版物并非旨在提供,也不构成TradingView提供或认可的任何形式的财务、投资、交易或其他类型的建议或推荐。请阅读使用条款了解更多信息。