Alpha Trading - Pseudo Laplace Z Score

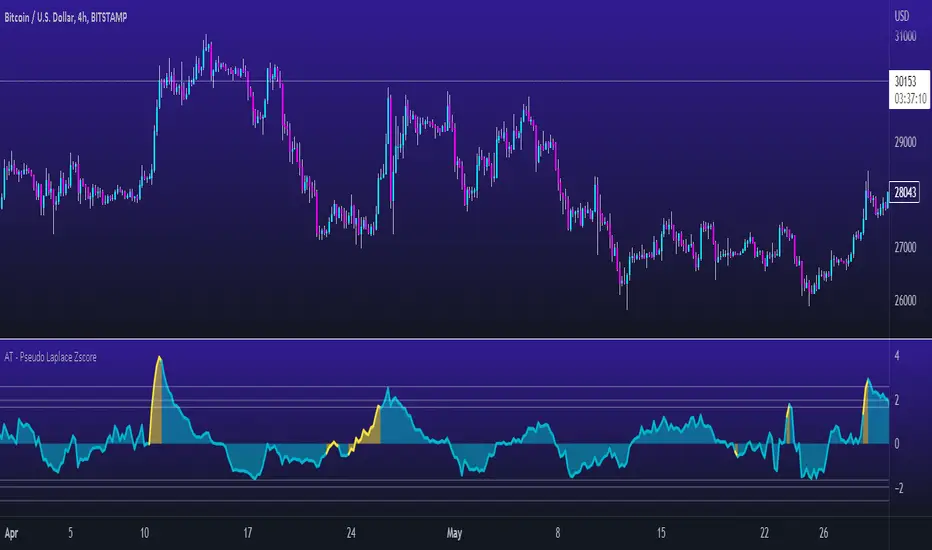
Alpha Trading - Pseudo Laplace Z Score

Slowly, very slowly a lot of quant and statistical methods have diffused the world of traditional technical analysis with the world of real math - VEPS (Volatility, Entropy, Probability and Statistics).
‘Alpha Trading' is showing the world how VEPS can show the best probabilities of success with your trading journey.
We send a big thank you to tradingview platform and pine coding team, for this great platform and the possibility to show the methods to trade with quant and statistical methods.
There appears to be resistance in the industry about these methods, so it is even more important now than ever, to support this awesome platform and amazing talented team at trading view and pine coders who enable us all with this wonderful platform to produce tools based on VEPS (Volatility, Entropy, Probability and Statistics).

The newest indicator from the Alpha Trading stable is the “Pseudo Laplace Z Score” which combines the established statistical method of z score applied on asset data. Which is based on our previous indicator called the “Alpha Trading – RMS-Z score”. We have made some optimizations, to give an even better fit to the specific returns of price. Optimizations are on the observation that returns are more Laplace distributed than Normal distributed.


figure 1: pink distribution of the real signal (BTC, 2D), gray is perfect theoretical Laplace distribution.

Therefore, the data is not Normal distributed, but Laplace distributed. Our new indicator calculates the real Z-Score of an underlying asset.

As Z Score is a standardized Normal distribution, it relies upon the definition of Normal distribution. If it deviates from this, it still can give useful information, but the absolute value (distance from the mean in standard deviations) is not reliable, and therefore the use of Normal distribution has some uncertainties.

Therefore, this indicator calculates a pseudo standard deviation, based on the Laplace distribution formulas and the relating Z Score.

By looking at the resulting distribution of the indicator itself, it is close to a perfect theoretical Normal distribution. It is much closer to the theoretical curve (gray), and thus indicates that the use of this approach is correct. Now we can show absolute values (i.e. distance to mean, in standard deviations) which can thus be considered to assist in determining the probabilities with your trading.


figure 2: distribution of indicator AT - Pseudo Laplace Z Score vs a theoretical perfect Normal distribution on BTC 4h


Looking at the indicator directly, it appears that the probability of 99% is crossed very rarely, like expected. Because only 1% of all candles we would expect this probability line to be exceeded.


figure 3: BTC 8h with AT-Pseudo Laplace Z Score

Coming back to the method of a Z Score in general. What is a Z-Score?
A Z-score is a numerical measurement that describes a value's relationship to the mean of a group of values. Z-score is measured in terms of standard deviations from the mean. If a Z-score is 0, it indicates that the data point's score is identical to the mean score. A Z-score of 1.0 would indicate a value that is one standard deviation from the mean. Z-scores may be positive or negative, with a positive value indicating the score is above the mean and a negative score indicating it is below the mean.

Simply put, a z-score (also called a standard score) gives you an idea of how far from the mean a data point is.

Basic guidelines How to Use this indicator:

• Consider Entering a Long Position when the indicator is low. Best moves are generally when the indicator Turns yellow(outlier)
  
• Consider Entering a Short Position when the indicator is high. Best moves are generally when the indicator Turns yellow(outlier)
  
• Consider the 3 confidence interval lines (gray lines) at 90%, 95%, and 99%, as possible reversal point (with related probability that it is not getting exceeded 🡪 reversal)